Self Organizing Maps
Stepping through the algorithm:1. Randomize the map's nodes' weight vectors
2. Grab an input vector
3. Traverse each node in the map
a) Use Euclidean distance formula to find similarity between the input vector and the map's node's weight vector
b) Track the node that produces the smallest distance (this node is the best matching unit, BMU)
4. Update the nodes in the neighbourhood of BMU by pulling them closer to the input vector
Wv(t + 1) = Wv(t) + Θ(t)α(t)(D(t) - Wv(t))
5. Increment t and repeat from 2 while t < λ
I am fascinated with SOM for two reasons:
- It really works! (Though some people are dissatisfied that they cannot find the energetic function that SOM minimizes. But what for do we need to know the energetic function when the algorithm is unsupervised?)
- The number of architectures and the possibility of creating new ones is really astonishing. That is much better than in MLP (don't mention even RBF), where almost all the architectures are created within a common framework that can be described by the same connection matrix and only very few constructive schemes have been widely accepted.
More:
- How SOM works
- Matlab NN Toolbox
- A simplified taxonomy of SOM networks
- Data Visualization with SOM and MDS
- The idea of various non-recurrent SOM models can be found in: R.T.Freeman, Hujun Yin, "Adaptive topological tree structure for document organization and visualization", Neural Networks, 12/2004
- The idea of various recurrent SOM models was presented e.g. in: M. Stricker, B. Hammer, "Unsupervised Recursive Sequence Processing", Neural Networks, 12/2004
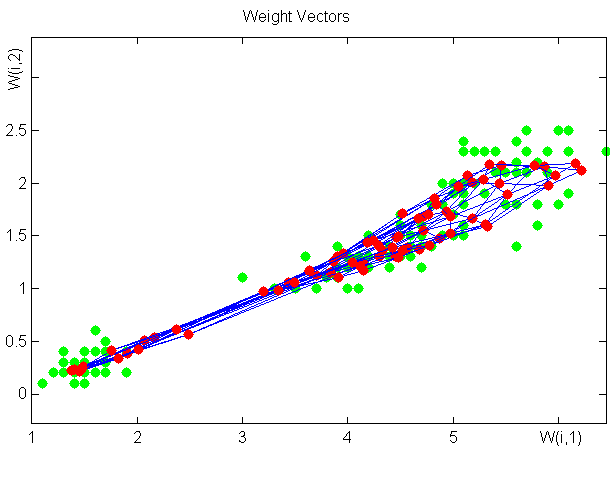
SOM training with Matlab NN Toolbox
Save the third and fourth column of the data section from mknn/iris.txt into i34.txt (in ANSI not UTF-8 encoding !)>> load 'i34.txt'
>> net = newsom([0 6; 0 6;] , [6 6]);
>> plot(i34(:,1),i34(:,2),'.g','markersize',20)
>> hold on
>> plotsom(net.iw{1,1},net.layers{1}.distances)
>> net.trainParam.epochs = 100;
>> net = train(net,transpose(i34));
TRAINR, Epoch 0/100
TRAINR, Epoch 25/100
TRAINR, Epoch 50/100
TRAINR, Epoch 75/100
TRAINR, Epoch 100/100
TRAINR, Maximum epoch reached.
>> plotsom(net.iw{1,1},net.layers{1}.distances)
A simplified taxonomy of SOM networks
-
fixed structure SOM
- standard SOM (1, 2 or 3-dimensional)
- quasi-four dimensional SOM
- hyperbolic SOM
- ...
-
growing SOMS
- GG - growing grid
- IGG - incremental growing grid
- GSOM - growing SOM
- GCS - growing cell structures
- Tree GCS
- ...
-
hierarchical SOMS
- HSOM - hierarchical SOM
- ...
-
growing hierarchical SOMS
- GHSOM - growing hierarchical SOM
- AHIGG - adaptive hierarchical growing grid
- HG-HSOM - hierarchically growing hyperbolic SOM
- ...
-
SOMS without grid
- Neural Gas
- Stochastic Relaxation
- Soft Competition Scheme
- ...
-
recurrent SOMS (for sequence analysis)
- TKM - temporal Kohonen map
- RSOM - recurrent SOM
- RecSOM - recursive SOM
- SOMSD - SOM for structured data
- MSOM - Merge SOM (or better Marc's SOM, as told me Marc Stricker, who was developing MSOM in his PhD thesis)
- ...
-
many hybrids, such as:
- Kangas map
- counter-propagation networks
- AR-SOM - SOM of competing autoregressive models
- ...
Miroslaw Kordos
Creatice Commons License. You are free to copy, share and adapt all articles and software from my web page for noncommercial purposes, provided that you attribute the work to me and place a link to my home page. What you build upon my works may be distributed only under the same or similar license and you may not distort the meaning of my original texts.
